进制转换进制转换本质我们使用短除法将十进制转换成二进制

“数制”只是一套符号系统来表示指称“量”的多少

我们用“1”这个符号来表示一个这一“量”的概念

自然界的“量”是无穷的，我们不可能为每一个“量”都造一个符号，这样的系统没人记得住

所以必须用有限的符号按一定的规律进行排列组合来表示这无限的“量”

符号是有限的，这些符号按照某种规则进行排列组合的个数是无限的

十进制是10个符号的排列组合，二进制是2个符号的排列组合

在进行进制转换时有一基本原则：转换后表达的“量”的多少不能发生改变

二进制中的111个苹果和十进制中的7个苹果是一样多的

十进制中的数位排列是这样的…… 万 千 百 十 个 十分 百分 千分……R进制中的数位排列是这样的……R^4 R^3R^2 R^1 R^0 R^-1 R^-2 R^-3……可以看出相邻的数位间相差进制的一次方

以下部分来源：知乎网友进制这事儿，说到底就是位值原理，即：同一个数字，放在不同的数位上，代表不同大小的“量”

例如：十进制中，百位上的1表示100，十位上的1表示10

任何进制中，每个数都可以按位权展开成各个数位上的数字乘以对应数位的位权，再相加的形式，如：十进制的123=1×100+2×10+3×1十进制的9876=9×1000+8×100+7×10+6×1问：为啥相应的数位是1000、100、10、1？为啥不是4、3、2、1？答：十进制，满十进一，再满十再进一，因此要想进到第三位，得有10×10；第4位得有10×10×10这样我们就知道了：对10进制，从低位到高位，依次要乘以10^0，10^1,10^2,10^3……，也就是1、10、100、1000对2进制，从低位到高位，依次要乘以2^0，2^1,2^2,2^3……，也就是1、2、4、8、……下面我们开始转换进制（以十进制换成二进制为例）：原来十进制咱们的数位叫 千位、百位、十位……现在二进制数位变成了八位、四位、二位……模仿上面十进制按位权展开的方式，把二进制数1011按权展开： 1011=1×2^3+0×2^2+1×2^1+1×2^0=1×8+0×4+1×2+1×1=8+2+1=11接下来我们进行十进制往二进制的转换：比较小的数，直接通过拆分就可以转换回去比如13，我们把数位摆好八位、四位、二位，不能写十六了，因为一旦“十六”那个数位上的符号是“1”，那就表示有1个16，即便后面数位上的符号全部是“0”，把这个二进制数按权位展开后，在按照十进制的运算规律计算，得到的数也大于13了

那最多就只能包含“八”这个数位

13-8=5，5当中有4，5-4=1好啦，我们知道13=1*8+1*4+0*2+1*1 把“1”、“1”、“0”“1”这几个符号放到数位上去：八位、四位、二位、一位1 1 0 1于是十进制数13=二进制数1101现在你按照书上说的短除法来试试，会发现它和你凑数得到的结果刚好是一样的，为什么短除法可以实现进制的转换呢？为什么每次要除以进制呢？为什么要把余数倒着排列呢？想要知道其中的道理的话，请仔细品味以下的递归原理（不知道递归没关系）：（1）一个十进制数321的末尾是1，意味着一定是……+1，省略号部分一定是10的倍数，所以一个十进制数末尾是1意味着十进制数除以进制10一定余1

所以第一次除以10之后的余数，应该放在十进制的最后一个数位“个位”，也就是说个位上的符号是1

类比，一个二进制数111（注意，数值不等于上面十进制的111）末尾是1，意味着一定是……+1，前面的省略号部分都是2的倍数

所以一个二进制数末尾是1，意味着它对应的十进制数除以进制2一定余1

所以第一次除以2之后的余数，应该放在二进制的最后一个数位“一位”，也就是说一位上的符号是1

（2）如果一个十进制数321“十位”是2，我们希望把它转换为（1）的情况

那么我们把这个十进制数的末尾抹掉，也就是减去“个位”上的1，再除以进制10，得到32

这样原来“十位”上的“2”就掉到了“个位”上

再把32做（1）的处理

类比，如果一个二进制数111“二位”是1，我们希望把它转换为（1）的情况，那么我们把这个二进制数的末尾抹掉，也就是减去“一位”上的1，再除以进制2，得到11

这样原来“二位”上的“1”就掉到了“一位”上

再把11做（1）的处理

总结：其实这个过程就是把各个数位上的符号求出来的过程

现在你应该可以回答以下问题了：为什么短除法可以实现进制的转换呢？为什么每次要除以进制呢？为什么要把余数倒着排列呢？R进制转换成十进制就是按权位展开，把展开式放到十进制下，再按照“十进制”的运算规律计算

因为是十进制，所以就允许使用2、3、4、5、6、7、8、9了

所以2的n次方就不用写成指数，而可以用另外的八个符号来表示了

十进制--->二进制对于整数部分，用被除数反复除以2，除第一次外，每次除以2均取前一次商的整数部分作被除数并依次记下每次的余数

另外，所得到的商的最后一位余数是所求二进制数的最高位

对于小数部分，采用连续乘以基数2，并依次取出的整数部分，直至结果的小数部分为0为止

故该法称“乘基取整法”

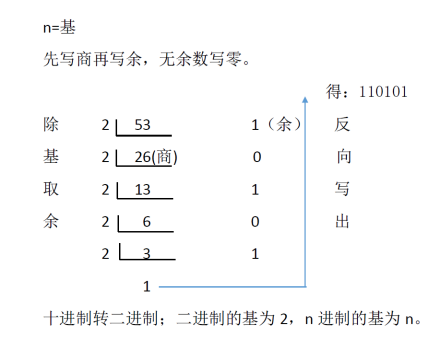
给你一个十进制，比如：6，如果将它转换成二进制数呢？10进制数转换成二进制数，这是一个连续除以2的过程：把要转换的数，除以2，得到商和余数，将商继续除以2，直到商为0

最后将所有余数倒序排列，得到数就是转换结果

听起来有些糊涂？结合例子来说明

比如要转换6为二进制数

“把要转换的数，除以2，得到商和余数”

那么：要转换的数是6， 6 ÷ 2，得到商是3，余数是0

“将商继续除以2,直到商为0……”现在商是3，还不是0，所以继续除以2

那就： 3 ÷ 2, 得到商是1,余数是1

“将商继续除以2，直到商为0……”现在商是1，还不是0，所以继续除以2

那就： 1 ÷ 2, 得到商是0，余数是1“将商继续除以2，直到商为0……最后将所有余数倒序排列”好极！现在商已经是0

我们三次计算依次得到余数分别是：0、1、1，将所有余数倒序排列，那就是：110了！6转换成二进制，结果是110

把上面的一段改成用表格来表示，则为：被除数计算过程商余数66/23033/21111/201（在计算机中，÷用 / 来表示）二进制--->十进制二进制数转换为十进制数二进制数第0位的权值是2的0次方，第1位的权值是2的1次方……所以，设有一个二进制数：0110 0100，转换为10进制为：下面是竖式：0110 0100 换算成十进制从右往左开始换算第0位 0 * 20 = 0第1位 0 * 21 = 0第2位 1 * 22 = 4第3位 0 * 23 = 0第4位 0 * 24 = 0第5位 1 * 25 = 32第6位 1 * 26 = 64第7位 0 * 27 = 0公式：第N位2(N)---------------------------100用横式计算为：0 * 20 + 0 * 21 + 1 * 22 + 0 * 23 + 0 * 24 + 1 * 25 + 1* 26 + 0 * 27 = 100除0以外的数字0次方都是1，但0乘以多少都是0，所以我们也可以直接跳过值为0的位：1 * 22 + 1 * 25 +1*26 = 100十进制--->八进制10进制数转换成8进制的方法，和转换为2进制的方法类似，唯一变化：除数由2变成8

来看一个例子，如何将十进制数120转换成八进制数

用表格表示：被除数计算过程商余数120120/81501515/81711/801120转换为8进制，结果为：170

八进制--->十进制八进制就是逢8进1

八进制数采用 0～7这八数来表达一个数

八进制数第0位的权值为8的0次方，第1位权值为8的1次方，第2位权值为8的2次方……所以，设有一个八进制数：1507，转换为十进制为：用竖式表示：1507换算成十进制

第0位 7 * 80 = 7第1位 0 * 81 = 0第2位 5 * 82 = 320第3位 1 * 83 = 512--------------------------839同样，我们也可以用横式直接计算：7 * 80 + 0 * 81 + 5 * 82 + 1 * 83 = 839结果是，八进制数 1507 转换成十进制数为 839十进制--->十六进制10进制数转换成16进制的方法，和转换为2进制的方法类似，唯一变化：除数由2变成16

同样是120，转换成16进制则为：被除数计算过程商余数120120/167877/1607120转换为16进制，结果为：78

十六进制--->十进制16进制就是逢16进1，但我们只有0~9这十个数字，所以我们用A，B，C，D，E，F这六个字母来分别表示10，11，12，13，14，15

字母不区分大小写

十六进制数的第0位的权值为16的0次方，第1位的权值为16的1次方，第2位的权值为16的2次方……所以，在第N（N从0开始）位上，如果是是数 X （X 大于等于0，并且X小于等于 15，即：F）表示的大小为 X * 16的N次方

假设有一个十六进数 2AF5, 那么如何换算成10进制呢？用竖式计算：2AF5换算成10进制:第0位： 5 * 160 = 5第1位： F * 161 = 240第2位： A * 162 = 2560第3位： 2 * 163 = 8192-------------------------------------10997直接计算就是：5 * 160 + F * 161 + A * 162 + 2 * 163 = 10997(别忘了，在上面的计算中，A表示10，而F表示15)现在可以看出，所有进制换算成10进制，关键在于各自的权值不同

假设有人问你，十进数 1234 为什么是 一千二百三十四？你可以给他这么一个算式：1234 = 1 * 103 + 2 * 102 + 3 * 101 + 4 * 100二进制--->八进制（11001.101）（二）整数部分： 从后往前每三位一组，缺位处用0填补，然后按十进制方法进行转化， 则有：001=1011=3然后我们将结果按从下往上的顺序书写就是：31，那么这个31就是二进制11001的八进制形式八进制--->二进制（31.5）（八）整数部分：从后往前每一位按十进制转化方式转化为三位二进制数，缺位处用0补充 则有：1---->1---->0013---->11然后我们将结果按从下往上的顺序书写就是：11001，那么这个11001就是八进制31的二进制形式二进制--->十六进制二进制和十六进制的互相转换比较重要

不过这二者的转换却不用计算，每个C，C++程序员都能做到看见二进制数，直接就能转换为十六进制数，反之亦然

我们也一样，只要学完这一小节，就能做到

首先我们来看一个二进制数：1111，它是多少呢？你可能还要这样计算：1 * 20 + 1 * 21 + 1 * 22 + 1 * 23 = 1 * 1 + 1 * 2 + 1 * 4 + 1 * 8 = 15

然而，由于1111才4位，所以我们必须直接记住它每一位的权值，并且是从高位往低位记，：8、4、2、1

即，最高位的权值为23 = 8，然后依次是 22 = 4，21=2， 20 = 1

记住8421，对于任意一个4位的二进制数，我们都可以很快算出它对应的10进制值

下面列出四位二进制数xxxx 所有可能的值（中间略过部分）仅四位的二进制数快速计算方法十进制值十六进制值11118+4+2+115F11108+4+2+014E11018+4+0+113D11008+4+0+012C10118+0+2+111B10108+0+2+010A10018+0+0+199……00010+0+0+11100000+0+0+000二进制数要转换为十六进制，就是以4位一段，分别转换为十六进制

如：二进制数1111 11011010 01011001 1011对应的十六进制数FDA59B十六进制--->二进制反过来，当我们看到 FD时，如何迅速将它转换为二进制数呢？先转换F：看到F，我们需知道它是15（可能你还不熟悉A～F这六个数），然后15如何用8421凑呢？应该是8 + 4 + 2 + 1，所以四位全为1 ：1111

接着转换 D：看到D，知道它是13，13如何用8421凑呢？应该是：8 + 4 + 1,即：1101

所以,FD转换为二进制数，为： 1111 1101由于十六进制转换成二进制相当直接，所以，我们需要将一个十进制数转换成2进制数时，也可以先转换成16进制，然后再转换成2进制

比如，十进制数 1234转换成二制数，如果要一直除以2，直接得到2进制数，需要计算较多次数

所以我们可以先除以16，得到16进制数:被除数计算过程商余数12341234/167727777/16413(D)44/1604结果16进制为： 0x4D2然后我们可直接写出0x4D2的二进制形式： 0100 1101 0010

其中对映关系为：0100 -- 41101 -- D0010 -- 2同样，如果一个二进制数很长，我们需要将它转换成10进制数时，除了前面学过的方法是，我们还可以先将这个二进制转换成16进制，然后再转换为10进制

下面举例一个int类型的二进制数：01101101 11100101 10101111 00011011我们按四位一组转换为16进制： 6D E5 AF 1B再转换为10进制：6*167+D*166+E*165+5*164+A*163+F*162+1*161+B*160=1,843,769,115十进制--->负进制下面是将十进制数转换为负R进制的公式：N=(dmdm-1...d1d0)-R=dm*(-R)m+dm-1*(-R)m-1+...+d1*(-R)1+d0*(-R)015=1*(-2)4+0*(-2)3+0*(-2)2+1*(-2)1+1*(-2)0=10011(-2)

以上内容由大学时代综合整理自互联网，实际情况请以官方资料为准。