tarjan算法算法介绍如果两个顶点可以相互通达，则称两个顶点强连通(strongly connected)

如果有向图G的每两个顶点都强连通，称G是一个强连通图

有向图的极大强连通子图，称为强连通分量(strongly connected components)

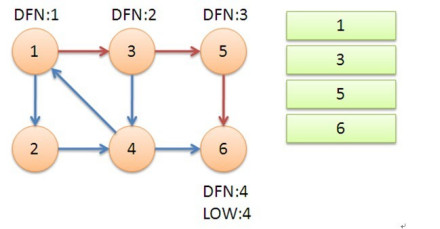
图1中，子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达

{5},{6}也分别是两个强连通分量

Tarjan算法是用来求有向图的强连通分量的

求有向图的强连通分量的Tarjan算法是以其发明者Robert Tarjan命名的

Robert Tarjan还发明了求双连通分量的Tarjan算法

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树

搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量

定义DFN(u)为节点u搜索的次序编号(时间戳)，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号

当DFN(u)=Low(u)时，以u为根的搜索子树上所有节点是一个强连通分量

接下来是对算法流程的演示

从节点1开始DFS，把遍历到的节点加入栈中

搜索到节点u=6时，DFN=LOW，找到了一个强连通分量

退栈到u=v为止，{6}为一个强连通分量

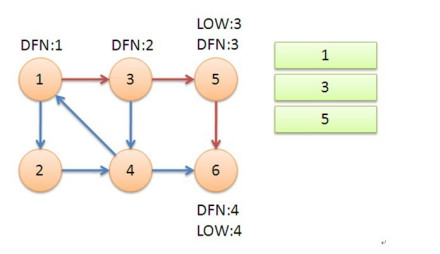
返回节点5，发现DFN=LOW，退栈后{5}为一个强连通分量

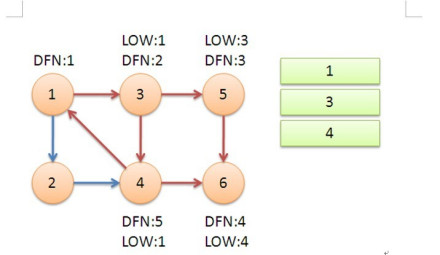
返回节点3，继续搜索到节点4，把4加入堆栈

发现节点4向节点1有后向边，节点1还在栈中，所以LOW=1

节点6已经出栈，(4,6)是横叉边，返回3，(3,4)为树枝边，所以LOW=LOW=1

继续回到节点1，最后访问节点2

访问边(2,4)，4还在栈中，所以LOW=DFN=5

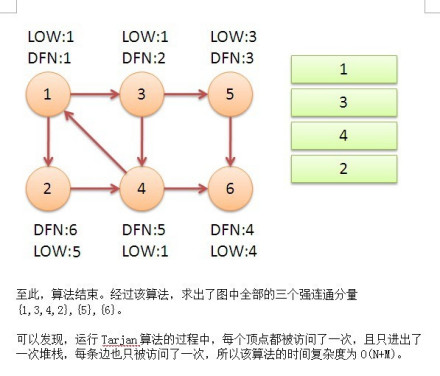
返回1后，发现DFN=LOW，把栈中节点全部取出，组成一个连通分量{1,3,4,2}

至此，算法结束

经过该算法，求出了图2中全部的三个强连通分量{1,3,4,2},{5},{6}

可以发现，运行Tarjan算法的过程中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为O(N+M)

以上内容由大学时代综合整理自互联网，实际情况请以官方资料为准。