欧几里得算法算法原理Lemma 1.3.1 若 a,b 且 a = bh + r，其中 h,r，则 gcd(a,b) = gcd(b,r)

 证 明. 假设 d1 = gcd(a,b) 且 d2 = gcd(b,r)， 证明 d1| d2 且 d2| d1，因而可利用 Proposition 1.1.3⑵ 以及 d1,d2 皆为正数得证 d1 = d2

因 d1| a 且 d1| b 利用 Corollary 1.1.2 知 d1| a - bh = r. 因为 d1| b,d1| r 且 d2 = gcd(b,r) 故由 Proposition 1.2.5 知 d1| d2. 另一方面，因为 d2| b 且 d2| r 故 d2| bh + r = a. 因此可得 d2| d1

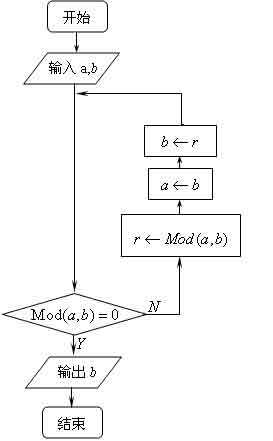
Lemma 1.3.1 告诉当 a > b > 0 时，要求 a,b 的最大公因数我们可以先将 a 除以 b 所得余数若为 r，则 a,b 的最大公因数等于 b 和 r 的最大公因数. 因为 r < b < a，所以当然把计算简化了，接着我们就来看看辗转相除法. 由于 gcd(a,b) = gcd(- a,b) 所以我们只要考虑 a,b 都是正整数的情况

Theorem 1.3.2 (The Euclidean Algorithm) 假设 a,b 且 a > b. 由除法原理知存在 h0,r0 使得a = bh0 + r0，其中 r0 < b.若 r0 > 0，则存在 h1,r1 使得b = r0h1 + r1，其中 0r1 < r0.若 r1 > 0，则存在 h2,r2 使得r0 = r1h2 + r2，其中 0r2 < r1.如此继续下去直到 rn = 0 为止，若 n = 0 （即 r0 = 0），则 gcd(a,b) = b. 若 n1，则 gcd(a,b) = rn - 1

证 明. 首先注意若 r0 0，由于 r0 > r1 > r2 > ... 是严格递减的，因为 r0 和 0 之间最多仅能插入 r0 - 1 个正整数，所以我们知道一定会有 nr0 使得 rn = 0

若 r0 = 0，即 a = bh0，故知 b 为 a 之因数，得证 b 为 a,b 的最大公因数

若 r0 > 0，则由 Lemma 1.3.1 知gcd(a,b) = gcd(b,r0) = gcd(r0,r1） = ... = gcd(rn - 1,rn) = gcd(rn - 1,0) = rn - 1

我们来看用辗转相除法求最大公因数的例子Example 1.3.3 我们求 a = 481 和 b = 221 的最大公因数

首先由除法原理得 481 = 2 . 221 + 39，知 r0 = 39. 因此再考虑 b = 221 除以 r0 = 39 得 221 = 5 . 39 + 26，知 r1 = 26，再以 r0 = 39 除以 r1 = 26 得 39 = 1 . 26 + 13，知 r2 = 13

最后因为 r2 = 13整除r1 = 26 知 r3 = 0，故由 Theorem 1.3.2 知 gcd（481,221） = r2 = 13

在利用辗转相除法求最大公因数时，大家不必真的求到 rn = 0，例如在上例中可看出 r0 = 39 和 r1 = 26 的最大公因数是 13，利用 Lemma 1.3.1 马上得知 gcd(a,b) = 13

在上一节 Corollary 1.2.5 告诉我们若 gcd(a,b) = d，则存在 m,n 使得 d = ma + nb

当时我们没有提到如何找到此 m,n， 我们利用辗转相除法来介绍一个找到 m,n 的方法， 我们沿用 Theorem 1.3.2 的符号，看 r0 = 0 的情形，此时 d = gcd(a,b) = b 所以若令 m = 0,n = 1，则我们有 d = b = ma + nb. 当 r0 0 但 r1 = 0 时，我们知 d = gcd(a,b) = r0

故利用 a = bh0 + r0 知，若令 m = 1,n = - h0，则 d = r0 = ma + nb

同理若 r0 0,r1 0 但 r2 = 0，则知 d = gcd(a,b) = r1

故利用 a = bh0 + r0 以及 b = r0h1 + r1 知r1 = b - r0h1 = b - (a - bh0)h1 = - h1a + （1 + h0h1）b

因此若令 m = - h1 且 n = 1 + h0h1，则 d = r1 = ma + nb. 依照此法，当 r0,r1 和 r2 皆不为 0 时，由于 d = gcd(a,b) = rn - 1 故由 rn - 3 = rn - 2hn - 1 + rn - 1 知 d = rn - 3 - hn - 1rn - 2. 利用前面推导方式我们知存在 m1,m2,n1,n2 使得 rn - 3 = m1a + n1b 且 rn - 2 = m2a + n2b 故代入得d = (m1a + n1b) - hn - 1(m2a + n2b) = (m1 - hn - 1m2）a + (n1 - hn - 1n2）b.因此若令 m = m1 - hn - 1m2 且 n = n1 - hn - 1n2，则 d = ma + nb.上面的说明看似好像当 r0 0 时对每一个 i {0,1,...,n - 2} 要先将 ri 写成 ri = mia + nib，最后才可将 d = rn - 1 写成 ma + nb 的形式，其实这只是论证时的方便，在实际操作时我们其实是将每个 ri 写成 mi'ri - 2 + ni'ri - 1 的形式慢慢逆推回 d = ma + nb. 请看以下的例子.Example 1.3.4 我们试着利用 Example 1.3.3 所得结果找到 m,n 使得 13 = gcd（481,221） = 481m + 221n. 首先我们有 13 = r2 = 39 - 26 = r0 - r1. 而 r1 = 221 - 5 . 39 = b - 5r0，故得 13 = r0 - (b - 5r0) = 6r0 - b. 再由 r0 = 481 - 2 . 221 = a - 2b，得知 13 = 6(a - 2b) - b = 6a - 13b. 故得 m = 6 且 n = - 13 会满足 13 = 481m + 221n

要注意这里找到的 m,n 并不会是唯一满足 d = ma + nb 的一组解，虽然上面的推演过程好像会只有一组解，不过只能说是用上面的方法会得到一组解，并不能担保可找到所有的解，比方说若令 m' = m + b,n' = n - a，则 m'a + n'b = (m + b)a + (n - a)b = ma + nb = d. 所以 m',n' 也会是另一组解，所以以后当要探讨唯一性时，若没有充分的理由千万不能说由前面的推导过程看出是唯一的就断言是唯一，一般的作法是假设你有两组解，再利用这两组解所共同满足的式子找到两者之间的关系. 我们看看以下的作法

Proposition 1.3.5 假设 a,b 且 d = gcd(a,b)

若 x = m0,y = n0 是 d = ax + by 的一组整数解，则对任意 t,x = m0 + bt/d,y = n0 - at/d 皆为 d = ax + by 的一组整数解，而且 d = ax + by 的所有整数解必为 x = m0 + bt/d,y = n0 - at/d 其中 t 这样的形式

证 明. 假设 x = m,y = n 是 d = ax + by 的一组解， 由于已假设 x = m0,y = n0 也是一组解，故得 am + bn = am0 + bn0. 也就是说 a(m - m0) = b(n0 - n). 由于 d = gcd(a,b），我们可以假设 a = a'd,b = b'd 其中 a',b' 且 gcd(a',b') = 1 （参见 Corollary 1.2.3）

因此得 a'(m - m0) = b'(n0 - n)

利用 b'| a'(m - m0),gcd(a',b') = 1 以及 Proposition 1.2.7⑴ 得 b'| m - m0. 也就是说存在 t 使得 m - m0 = b't. 故知 m = m0 + b't = m0 + bt/d. 将 m = m0 + bt/d 代回 am + bn = am0 + bn0 可得 n = n0 - at/d，因此得证 d = ax + by 的整数解都是 x = m0 + bt/d,y = n0 - at/d 其中 t 这样的形式. 最后我们仅要确认对任意 t,x = m0 + bt/d,y = n0 - at/d 皆为 d = ax + by 的一组整数解， 然而将 x = m0 + bt/d,y = n0 - at/d 代入 ax + by 得 a(m0 + bt/d)+ b(n0 - at/d)= am0 + bn0 = d，故得证本定理

利用 Proposition 1.3.5 我们就可利用 Example 1.3.4 找到 13 = 481x + 221y 的一组整数解 x = 6,y = - 13 得到 x = 6 + 17t,y = - 13 - 37t 其中 t 是 13 = 481x + 221y 所有的整数解

以上内容由大学时代综合整理自互联网，实际情况请以官方资料为准。