欧几里得算法算法版本Swift 语言版本import Foundationfunc gcd(a: Int, b: Int) -> Int { var x = a, y = b while y != 0 { (x, y) = (y, x % y) } return x}let x = 75, y = 100let result = gcd(a: x, b: y)print("\(x) 和 \(y) 的最大公约数是 \(result)")Go语言版本package mainimport "fmt"func main() {    var x, y int = 18, 12     result := gcd(x,y)      fmt.Printf("x, y 的最大公约数是 : %d",result)}func gcd(x,y int) int{     for y != 0  {                 x, y = y, x%y       }      return x}Pascal语言版var  a,b,c:integer;begin  readln(a,b);  c:=a mod b;  while c<>0 do  begin    a:=b;b:=c;c:=a mod b;  end;  write(b);end.C语言版/*欧几里得算法：辗转求余原理： gcd(a,b)=gcd(b,a mod b)当b为0时，两数的最大公约数即为agetchar()会接受前一个scanf的回车符*/#include unsigned int MaxCommonFactor(int a,int b){ if(a % b == 0) return b; return MaxCommonFactor(b, a % b);} unsigned int Gcd(unsigned int M,unsigned int N){ unsigned int Rem; while(N > 0) { Rem = M % N; M = N; N = Rem; } return M;}int main(void){ int a,b; scanf("%d %d",&a,&b); printf("the greatest common factor of %d and %d is ",a,b); printf("%d\n",Gcd(a,b)); printf("recursion:%d\n",MaxCommonFactor(a,b)); return 0;}Ruby语言版#用欧几里得算法计算最大公约数(排版略）def gcd(x, y)if y == 0return xelsereturn gcd(y, x % y)endendC++版#include using namespace std;int gcd(int a, int b){ if (a % b==0) return b; else return gcd(b, a % b);}int x, y; int main(){ cin >> x >> y; cout << gcd(x, y); return 0;}Java版int gcd(int m,int n){   if(n == 0){        return m;     }    int r = m%n;    return gcd(n,r);}JavaScript版 function gcd(a, b) {        if (a % b == 0) return b;        return gcd(b, a % b);    }Python版def gcd(a, b):    while a != 0:        a, b = b % a, a    return b　Erlang版gcd(A, 0) -> A;gcd(A, B) -> gcd(B, A rem B).Rust版 pub fn gcd(x: u64, y: u64) -> u64 {       let remainder = x % y;       if remainder == 0 {           return y;       } else {           return gcd(y, remainder);       }    }    #[cfg(test)]    mod tests {    use super::*;    #[test]    fn gcd_works() {    assert_eq!(gcd(2, 4), 2);           assert_eq!(gcd(6, 27), 3);    assert_eq!(gcd(4, 2), 2);    assert_eq!(gcd(27, 6), 3);       }    }Bash版function gcd() { if [ ! -n "$2" ];then return fi if [ "$2" == "0" ];then echo "$1" return fi gcd "$2" "$[$1%$2]"}模P乘法逆元对于整数a、p，如果存在整数b，满足ab mod p =1，则说，b是a的模p乘法逆元

定理：a存在模p的乘法逆元的充要条件是gcd(a，p) = 1证明：首先证明充分性如果gcd(a，p) = 1，根据欧拉定理，aφ（p) ≡ 1 mod p，因此显然aφ（p)-1 mod p是a的模p乘法逆元

再证明必要性假设存在a模p的乘法逆元为bab ≡ 1 mod p则ab = kp +1 ，所以1 = ab - kp因为gcd(a，p) = d所以d | 1所以d只能为1Stein算法欧几里得算法是计算两个数最大公约数的传统算法，他无论从理论还是从效率上都是很好的

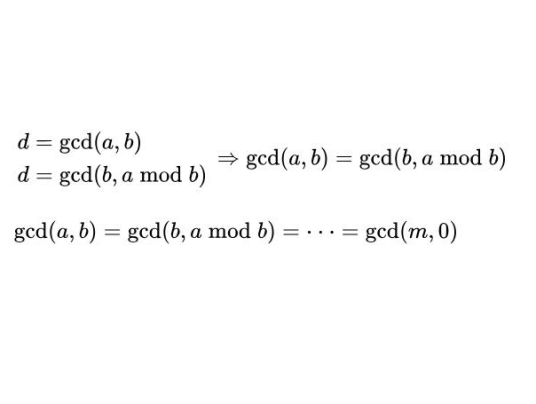
但是他有一个致命的缺陷，这个缺陷只有在大素数时才会显现出来

硬件平台，一般整数最多也就是64位，对于这样的整数，计算两个数之间的模是很简单的

对于字长为32位的平台，计算两个不超过32位的整数的模，只需要一个指令周期，而计算64位以下的整数模，也不过几个周期而已

但是对于更大的素数，这样的计算过程就不得不由用户来设计，为了计算两个超过 64位的整数的模，用户也许不得不采用类似于多位数除法手算过程中的试商法，这个过程不但复杂，而且消耗了很多CPU时间

对于现代密码算法，要求计算 128位以上的素数的情况比比皆是，设计这样的程序迫切希望能够抛弃除法和取模

Stein算法由J. Stein于1961年提出，这个方法也是计算两个数的最大公约数

和欧几里得算法不同的是，Stein算法只有整数的移位和加减法，这对于程序设计者是一个福音

为了说明Stein算法的正确性，首先必须注意到以下结论：gcd(a,a) = a，也就是一个数和他自身的公约数是其自身gcd(ka,kb) = k gcd(a,b），也就是最大公约数运算和倍乘运算可以交换，特殊的，当k=2时，说明两个偶数的最大公约数必然能被2整除C++/java 实现// c++/java stein 算法int gcd(int a,int b){if(ab{int temp = a;a = b;b=temp;}if(0==b) //the base casereturn a;if(a%2==0 && b%2 ==0) //a and b are evenreturn 2*gcd(a/2,b/2）；if (a%2 == 0) // only a is evenreturn gcd(a/2,b);if (b%2==0)// only b is evenreturn gcd(a,b/2）；return gcd((a-b)/2,b);// a and b are odd}算法扩展扩展欧几里得算法不但能计算(a，b）的最大公约数，而且能计算a模b及b模a的乘法逆元，用C语言描述如下：#include unsigned int gcdExtended( int a,  int b,  int *x,  int *y);int main(void) {    int  a, b,GCD;    int   x, y;    a = 1232, b = 573;    /*    gcdExtended(1232, 573)时, x = 20 and y = –43    1232x + 573y = 1    24640-24639 = 1    或者gcdExtended( 573,1232) 时,x=-43, y=20    573x+1232y = 1    -43*573+1232*20 = -24639+57640 = 1    gcdExtended(9151, 5787) 时    x=2011, y=-3180     */    GCD =  gcdExtended(a, b,&x, &y);    printf("gcdExtended(%d, %d) = %d, x=%d, y=%d\n", a, b, GCD,x,y);    return 0;}// 欧几里得扩展算法的C语言实现// ax+by=1unsigned int gcdExtended(int a, int b, int *x, int *y){    if (a == 0){        *x = 0;        *y = 1;        return b;    }    int x1, y1;    int gcd = gcdExtended(b%a, a, &x1, &y1);    *x = y1 - (b/a) * x1;    *y = x1;    return gcd;}扩展欧几里得算法对于最大公约数的计算和普通欧几里得算法是一致的

计算乘法逆元则显得很难明白

我想了半个小时才想出证明他的方法

首先重复拙作整除中的一个论断：如果gcd(a，b)=d，则存在m，n，使得d = ma + nb，称呼这种关系为a、b组合整数d，m，n称为组合系数

当d=1时，有 ma + nb = 1 ，此时可以看出m是a模b的乘法逆元，n是b模a的乘法逆元

为了证明上面的结论，我们把上述计算中xi、yi看成ti的迭代初始值，考察一组数（t1，t2，t3），用归纳法证明：当通过扩展欧几里得算法计算后，每一行都满足a×t1 + b×t2 = t3第一行：1 × a + 0 × b = a成立第二行：0 × a + 1 × b = b成立假设前k行都成立，考察第k+1行对于k-1行和k行有t1(k-1） t2(k-1） t3(k-1）t1(k) t2(k) t3(k)分别满足：t1(k-1） × a + t2(k-1） × b = t3(k-1）t1(k) × a + t2(k) × b = t3(k)根据扩展欧几里得算法，假设t3(k-1） = j t3(k) + r则：t3(k+1） = rt2(k+1） = t2(k-1） - j × t2(k)t1(k+1） = t1(k-1） - j × t1(k)则t1(k+1） × a + t2(k+1） × b=t1(k-1） × a - j × t1(k) × a +t2(k-1） × b - j × t2(k) × b= t3(k-1） - j t3(k) = r= t3(k+1）得证因此，当最终t3迭代计算到1时，有t1× a + t2 × b = 1，显然，t1是a模b的乘法逆元，t2是b模a的乘法逆元

以上内容由大学时代综合整理自互联网，实际情况请以官方资料为准。