更新过程定义定义一在数学上更新过程可简单地定义为相邻两个点事件(即更新)的间距是相互独立同分布(但从原点到第一次更新的间距T1可以有不同分布)的计数过程，根据T1的分布情形更新过程又分为普通更新过程，延迟更新过程和平衡更新过程三类，更新过程也可用过程的事件间距序列{Tn,n≥1}给定，这时N(t)和Tn有如下关系∶N(t)=sup{n:Sn≤t}和Sn=inf{t:N(t)=n}，其中是第n次更新时间(n≥1,再定义S0=0).对于普通更新过程,Sn是n个相互独立同分布的非负随机变量之和,因此在数学上更新过程也可以看做是一类特殊的独立随机变量和. 更新过程是Poisson过程的一种推广，其中事件发生的时间间隔是独立同分布的随机变量，分布函数为F ．定义二在故障报修方面的定义：如果假设故障间隔时问Xi= 一 ( =0)为来自某一分布的独立同分布样本，则随机过程Xi，i=1，2，…即为更新过程

其中，当故障间隔时间服从指数分布时，这一更新过程即为指数更新过程；当故障间隔时间服从Gamma分布时，这一更新过程即为Gamma更新过程

更新过程具有无记忆性，也就是说，对于一个更新过程，不管系统是全新的还是被修复了100次，下一次故障的实际都具有相同的分布，即更新过程描述了“修旧如新”维修效果

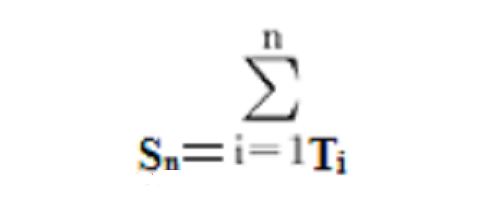
然而，需要注意的是，更新过程模型无法模拟通常在可修复系统中观测到的可靠性增长或可靠性衰减

对于更新过程模型，一个有用的指标是平均故障间隔时间(MTBF)，即故障间隔时间分布的均值．记为E(X) 

以上内容由大学时代综合整理自互联网，实际情况请以官方资料为准。