近日,电子信息与电气工程学院约翰·霍普克罗夫特计算机科学中心助理教授张宇昊针对网络规划问题的研究取得了重要进展,研究成果以“基于‘组连接性’的高可靠性网络规划问题”(Survivable Network Design Revisited: Group-Connectivity)为题被理论计算机科学领域国际顶级会议IEEE计算机科学基础年度研讨会(FOCS)接收。
该论文成功提出了首个“组对组”高连通性网络规划问题的非平凡近似算法。该成果与来自上海交通大学、上海财经大学理论计算机科学研究中心、加州大学默塞德分校的多位学者合作完成,得到了国家自然科学基金等项目的支持。
研究背景
网络规划问题即为如何建立一个满足需求连通性网络系统的问题。问题会给定一个图,连接不同网络节点的代价可能各有不同,节点的连接需求也可能各异。网络规划问题的目标即为如何用最小代价,满足输入所需的连接性。网络规划问题中有许多经典模型,根据不同灵活性的节点连接需求,分别有:最小生成树(要求所有节点互相连接),斯坦纳树(要求某节点集合互相连接),网络规划模型(可灵活输入需要连接的点对)。
然而在现实应用中,简单要求节点之间的“连接”并不足够。假如网络中的某些通路损坏,那么网络中所需的连通性就不复存在。因此,我们产生了如何构建高可靠的网络系统的需求。从理论角度,我们将节点之间的连接要求(存在一条通路),拓展为了高连通度要求(存在k条边不交的通路)。那么,即使当网络中有k-1条边被破坏,我们依然可以保证系统的连通性要求。在该模型中,我们可以根据调整输入中的k,来灵活应对不同可靠性场景的网络规划问题。
另一方面,上述模型均只关注了点与点之间的连通需求,但在一大类应用中,如集成电路设计、分布式数据中心,连通性需求可能会产生于组(节点集合)与组之间。由此,这需要我们进一步将点与点的连通需求,泛化到组与组之间。
本文综合研究以上种种需求的“组连接-网络规划(Group EC-SNDP)”模型,将高连接度和灵活的组连接需求,同时考虑进了建模中。
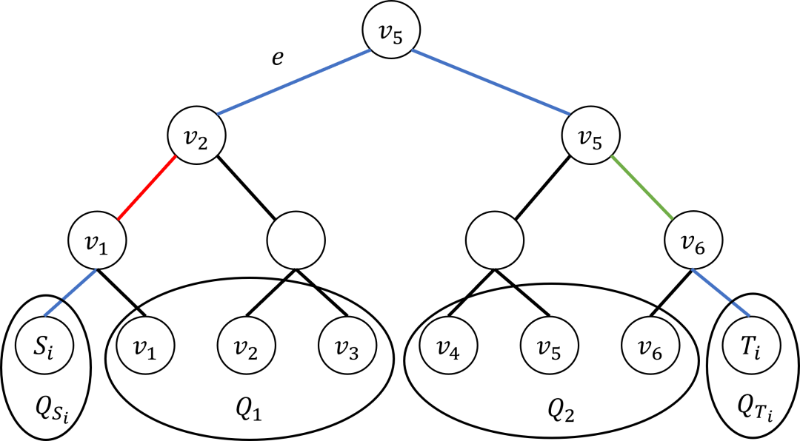
“组连接-网络规划(Group EC-SNDP)”模型
亮点成果
由于该模型是一个泛化程度很高的模型(同时考虑了高连接度和组连接需求),其研究难度会高于单纯考虑高连接度的点连接模型。在点连接模型中,如最小生成树、斯坦纳树、甚至是考虑高连接度的泛化网络规划模型,均存在比较成熟的算法结果。如最小生成树的多项式时间算法,斯坦纳树和高连接度的泛化网络规划模型的常数近似算法。但是组连接要求下的网络规划模型却迟迟没有出现任何成熟的近似算法。唯一的结果是2015年SODA会议中 Chalermsook,Grandoni,和Laekhanukit 三人发表的有损近似算法,该算法仅能输出接近模型要求的k连通度的结果,而不能真正达到模型要求。
本文利用连接度叠加技巧,基于线性规划舍入,结合了CGL2015 有损近似算法中对树上分数解的舍入技术和创新提出的分数解的阈值截断方法,成功提出了首个能够真正达到模型要求的k连通度的近似算法,并分析证明了算法的近似比。
关于FOCS
FOCS是由IEEE计算机学会的计算机数学基础专委会提供资助的计算机科学领域最顶级的国际会议,在整个理论计算机科学领域享有崇高的声望,并被公认属于难度最高的会议之一,与ACM计算理论年会(STOC)并称理论计算机科学两大顶会。
自1960年成立以来,FOCS历年会议涵盖的领域十分广泛,包括算法和数据结构、计算复杂性、密码学、计算几何、算法图论与组合学、计算随机性、计算博弈论和量子计算等。会议致力于为计算机理论的基础研究和新方法开创领域的研究者提供交流和展示的平台。

关于作者

张宇昊,上海交通大学约翰·霍普克罗夫特计算机科学中心助理教授,研究方向为理论计算机科学。本科毕业于浙江大学计算机系,2020年获得香港大学计算机科学博士学位,2021年加入上海交通大学约翰·霍普克罗夫特计算机科学中心。
论文链接:https://arxiv.org/abs/2204.13648
以上内容由大学时代综合整理自互联网,实际情况请以官方资料为准。