近期,上海交通大学廖世俊团队应用其提出的“精准数值模拟”(Clean Numerical Simulation,简称CNS),发现极其微小的数值噪音能够对二维Rayleigh–Bénard热对流这个可持续湍流的数值模拟结果产生宏观的影响。相关研究成果2022年9月在流体力学国际著名期刊Journal of Fluid Mechanics在线发表( https://doi.org/10.1017/jfm.2022.710 ),其第一作者秦石洁是博士生,廖世俊是通讯作者。
湍流,被称为经典力学的最后一个难题。湍流与航空、航天、海洋工程等许多领域都密切相关。深入研究湍流的生成和演化机理,具有重要的理论意义和应用价值。过去通常认为,源于热涨落或环境噪音的微小随机干扰可能在耗散尺度对湍流产生影响,但对湍流宏观流动的影响却不曾见报道。近期,廖世俊研究团队利用其提出的CNS,以二维湍流Rayleigh–Bénard热对流为例,对Navier–Stokes方程进行极高精度数值模拟(其数值噪音可忽略不计),并与传统方法(用RKwD表示)给出的数值结果(其数值噪音不可忽略)进行详细比较。研究发现,数值噪音不仅影响湍流的时空轨迹,而且对其统计结果也产生了显著影响。特别是,这些微小的随机干扰甚至会引起湍流宏观流动的定性变化:由CNS得到的精准模拟结果能够长期保持典型的旋涡状对流,但由传统算法(RKwD)给出的数值模拟却转变成剪切对流,其对应的流场变成一种带状湍流。
这项研究揭示了极其微小的扰动对湍流宏观流动之影响,丰富和加深了人们对湍流的认识和理解,具有重要的理论意义。同时,该研究也显示了CNS的有效性、新颖性和潜力。CNS为湍流研究提供了一个更加精确、可靠的工具。
廖世俊2009年首次提出CNS策略,以获得混沌动力系统可靠(收敛)的数值模拟。应用CNS,廖世俊及其学生曾成功求解了著名的三体问题周期解,将其周期解数量增加几个数量级,并率先提出求解三体问题周期解之路线图。详见报道: https://news.sjtu.edu.cn/jdzh/20220606/172074.html
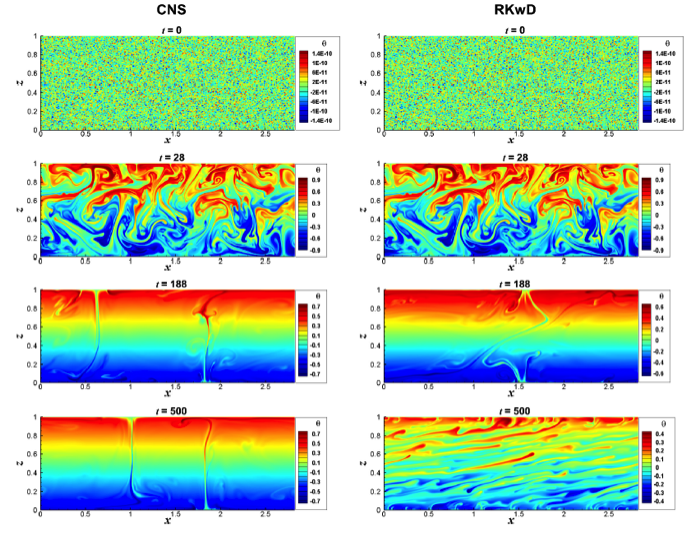
(与线性分布的背景温度场对比得到的)温度场偏差的演化。左图:通过CNS得到的精准模拟结果;右图:通过传统数值方法(RKwD)得到的结果。其对应动画如下
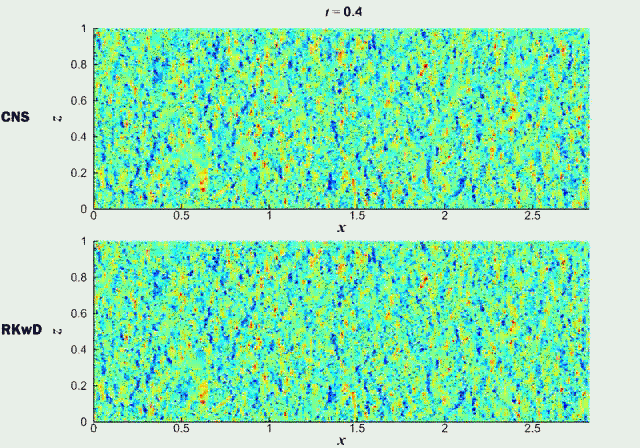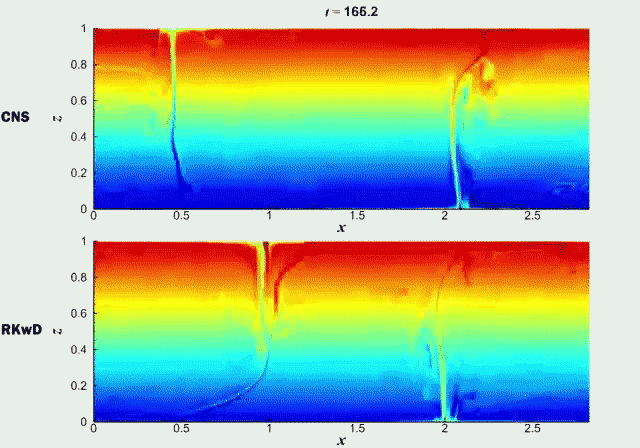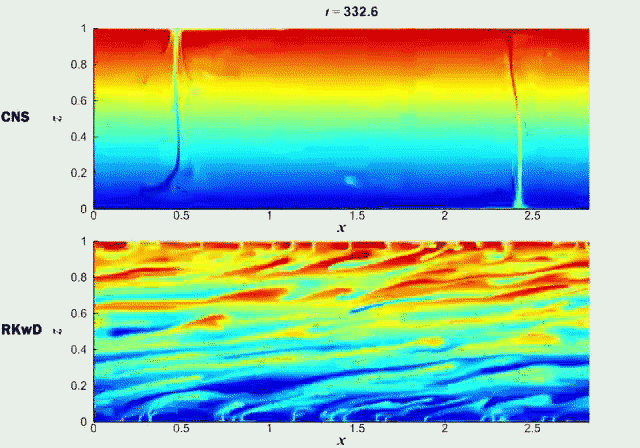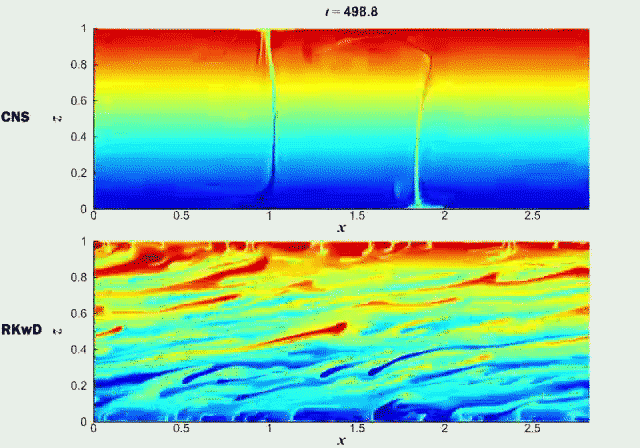
更多详情请阅原文:
S.J. Qin and S.J. Liao, “Large-scale influence of numerical noises as artificial stochastic disturbances on a sustained turbulence”, Journal of Fluid Mechanics, vol. 948, A7 (2022) (DOI: 10.1017/jfm.2022.710). [PDF] (Supplementary materials)
【作者简介】

秦石洁,上海交通大学,船舶海洋与建筑工程学院 博士生

廖世俊博士,上海交通大学,船舶海洋与建筑工程学院 讲席教授
以上内容由大学时代综合整理自互联网,实际情况请以官方资料为准。