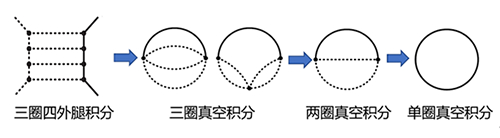
图 研究工作流程示意图

在国家自然科学基金项目（批准号：11875071、11975029）等资助下，北京大学马滟青研究员团队在微扰量子场论领域取得进展，解决了多圈费曼积分计算这一难题。成果以“仅用线性代数输入确定费曼积分（Determining Feynman Integrals with Only Input from Linear Algebra）”为题，于2022年11月23日发表在《物理评论快报》（Physical Review Letters）期刊。论文链接：https://doi.org/10.1103/PhysRevLett.129.222001。

从量子场论兴起以来，费曼积分作为微扰量子场论的基本单元，计算极其困难。理论学家一直被多圈费曼积分计算这一问题所困扰；部分情况下，即便双圈费曼积分的计算也难以完成。而在粒子物理领域，微扰量子场论与费曼积分的地位更是不可或缺，广泛用于缪子磁矩、大型强子对撞机希格斯粒子产率等的理论计算中；为了利用粒子物理实验数据检验标准模型和探测新物理信号，基于微扰量子场论的精确计算与理论预言需达到与实验数据可比拟的精度，为此需要计算大量极具挑战的多圈费曼积分。随着实验精度的不断提升，攻克多圈费曼积分计算成为粒子物理研究中的难题。

研究团队提出辅助质量流框架，利用线性代数首先把一般性费曼积分计算问题转换为“无外腿的真空积分”计算问题；在计算给定圈数的真空积分时，只需把少一圈的真空积分作为输入；不断循环这一过程，最终仅剩线性代数信息的输入；费曼积分计算问题被彻底简化为能够系统求解的线性代数问题，得到了计算多圈费曼积分的系统方法。由于该方法可计算任意时空维数下的费曼积分，团队进一步提出了提高微扰场论计算效率的新方案（图）。

以上内容由大学时代综合整理自互联网，实际情况请以官方资料为准。