电路元件集总参数模型由集总参数元件组成的电路称为集总参数电路或集总电路

在这种电路里，电流、电压除了在元件上应满足元件约束之外，还要满足基尔霍夫定律

对于图2a所示的集总参数电路，可以写出以下电路方程

基尔霍夫第一定律方程： i1=i2+i3基尔霍夫第二定律方程： u1+u2=us　u2=u3元件约束方程： u1=R1i1　u2=R2i2　u3=R3i3　us=f(t)这个电路的电路方程是一组代数方程

如果电路中还含有受控电源、理想变换器、运算放大器等元件，列出的电路方程仍然是一组代数方程

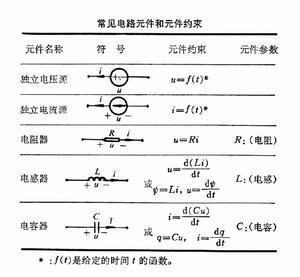
因为联系这些元件的电压和电流的元件约束是代数关系,不含对时间t的导数（如表<所示）

对于图2b电路，它的基尔霍夫定律方程和图2a电路的相同

若图的R、L、C是常数，即对应的元件是定常元件，则元件约束是： u1=Ri1　 　 us=f(t)由于电路里含有电容元件和电感元件，电路方程里有对时间t的导数

假设已知独立电压源的电压的时间变化即已知f(t)，已知图a 中三个定常电阻器的常值参数R1、R2、R3,或已知图b中三个定常元件的常值参数R、L、C,根据非齐次线性代数方程的理论或非齐次线性常系数常微分方程的理论，从原则上讲可以求解图a、图b各处的电流和电压

独立电压源的电压us以及独立电流源的电流is常称为激励，而其他的电流、电压叫做响应

当电路元件是时变的或者是非线性的，甚至既是时变、又是非线性的，求解电路方程很困难

一般需用计算机来解复杂的电路方程

以上内容由大学时代综合整理自互联网，实际情况请以官方资料为准。