第一数学归纳法例子假设我们要证明下面这个公式():其中 n 为任意自然数
这是用于计算前 n 个自然数的和的简单公式
证明这个公式成立的步骤如下
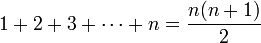
第一步是验证这个公式在 n = 1 时成立
我们有左边 = 1,而右边 = 1(1 + 1) / 2 = 1,所以这个公式在 n = 1 时成立
第一步完成
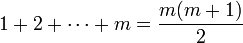
第二步第二步我们需要证明如果假设n = m 时公式成立,那么可以推导出 n = m+1 时公式也成立
证明步骤如下
我们先假设 n = m 时公式成立
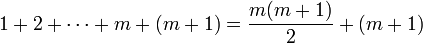
即(等式 1)然后在等式等号两边分别加上 m + 1 得到(等式 2)这就是 n = m+1 时的等式
我们需要根据等式 1 证明等式 2 成立
通过因式分解合并,等式 2 的右手边也就是说这样便证明了从 P(m) 成立可以推导出 P(m+1) 也成立
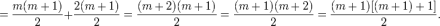
证明至此结束,结论:对于任意自然数 n,P(n) 均成立
以上内容由大学时代综合整理自互联网,实际情况请以官方资料为准。