函数一次函数在某一个变化过程中，设有两个变量x和y，如果可以写成 （k为一次项系数，b为常数），那么我们就说y是x的一次函数，其中x是自变量，y是因变量

特别的，当b=0时（ ），称y是x的正比例函数

基本性质：1、在正比例函数时，x与y的商一定（x≠0）

在反比例函数时，x与y的积一定

在y=kx+b（k，b为常数，k≠0）中，当x增大m时，函数值y则增大km，反之，当x减少m时，函数值y则减少km

2、当x=0时，b为一次函数图像与y轴交点的纵坐标，该点的坐标为（0，b）；当y=0时，一次函数图像与x轴相交于（﹣b/k）3、当b=0时，一次函数变为正比例函数

当然正比例函数为特殊的一次函数

4、在两个一次函数表达式中：当两个一次函数表达式中的k相同，b也相同时，则这两个一次函数的图像重合；当两个一次函数表达式中的k相同，b不相同时，则这两个一次函数的图像平行；当两个一次函数表达式中的k不相同，b不相同时，则这两个一次函数的图像相交；当两个一次函数表达式中的k不相同，b相同时，则这两个一次函数图像交于y轴上的同一点（0，b）；当两个一次函数表达式中的k互为负倒数时，则这两个一次函数图像互相垂直

5、两个一次函数（y1=k1x+b1,y2=k2x+b2）相乘时（k≠0），得到的的新函数为二次函数，该函数的对称轴为－（k2b1+k1b2）/（2k1k2）；当k1,k2正负相同时，二次函数开口向上；当k1,k2正负相反时，二次函数开口向下

二次函数与y轴交点为（0，b2b1）

6、两个一次函数（y1=ax+b,y2=cx+d）之比，得到的新函数y3=（ax+b）/（cx+d）为反比例函数，渐近线为x=－b/a，y=c/a

7、当平面直角坐标系中两直线平行时，其函数解析式中k的值（即一次项系数）相等；当平面直角坐标系中两直线垂直时，其函数解析式中k的值互为负倒数（即两个k值的乘积为-1）

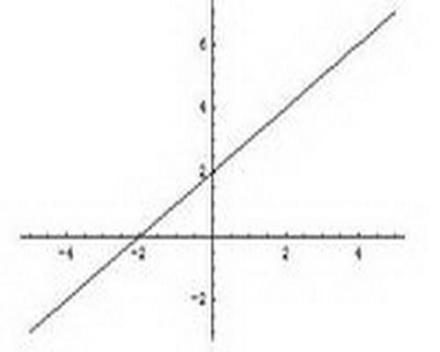
图像：如右图所示，一次函数y=kx+b（k≠0）图像是直线，过（0，b）和（-b/k，0）两点

特别地，当b=0时，图像过原点

一次函数和方程的联系与区别:1、一次函数和一元一次方程有相似的表达形式

2、一次函数表示的是一对（x，y）之间的关系，它有无数对解；一元一次方程表示的是未知数x的值，最多只有1个值

3、一次函数与x轴交点的横坐标就是相应的一元一次方程的根

一次函数和不等式:从函数的角度看，解不等式的方法就是寻求使一次函数y=kx+b的值大于（或小于）0的自变量x的取值范围的一个过程；从函数图像的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合

对应一次函数y=kx+b，它与x轴交点为（-b/k,0）

当k>0时，不等式kx+b>0的解为：x>- b/k，不等式kx+b<0的解为：x<- b/k；当k<0的解为：不等式kx+b>0的解为：x<- b/k，不等式kx+b<0的解为：x>- b/k 

以上内容由大学时代综合整理自互联网，实际情况请以官方资料为准。