动态算法工作原理动态算法所遵循的原则是最优性原理，它可描述如下：一个最优决策序列具有下述性质：无论初始状态和第一步决策是什么，余下的决策必须按照前一次决策所产生的新状态构成一个最优决策序列

也就是说，不论前面的状态和策略如何，后面的最优策略只取决于由最初策略所决定的当前状态

如果所求解问题的最优性原理成立，则说明用动态算法有可能解决该问题

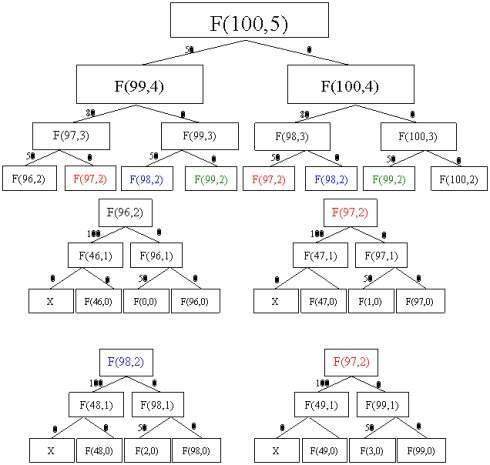
而解决问题的关键在于获取各阶段间的递推关系式

贝尔曼认为，利用最优性原理以及所获得的递推关系式去求解最优决策序列可以使枚举量急剧下降

动态算法的设计方法对于不同问题有不同的表达方式

这是由于各种问题的性质各不相同所造成的，所以，判定最优解的条件也不相同

因此，不存在一种通用的动态规划算法

如果存在一个决策序列，它包含有非局部最优的决策子序列时，该决策序列一定不是最优的

满足最优性原理的问题可以试着使用动态规划算法

然而，动态算法只是考察求解多阶段决策问题的一种途径，而不是一种特殊算法

不想线性规划那样，具有一个标准的数学表达式和明确的定义

无论是使用向前处理法还是使用向后处理法，都将所有子问题的最优解保存下来，这样做的目的是为了便于逐步递推得到原问题的最优解并避免对它们的重复计算

以上内容由大学时代综合整理自互联网，实际情况请以官方资料为准。