黄金分割数发展历史2000多年前,古希腊雅典学派的第三大算学家欧道克萨斯首先提出黄金分割

所谓黄金分割，指的是把长为L的线段分为两部分，使其中一部分对于全部之比，等于另一部分对于该部分之比

而计算黄金分割最简单的方法，是计算斐波契数列1，1，2，3，5，8，13，21，...后二数之比2/3,3/5,5/8,8/13,13/21,...近似值的

黄金分割在文艺复兴前后，经过阿拉伯人传入欧洲，受到了欧洲人的欢迎，他们称之为"金法"，17世纪欧洲的一位数学家，甚至称它为"各种算法中最可宝贵的算法"

这种算法在印度称之为"三率法"或"三数法则"，也就是我们现在常说的比例方法

其实有关"黄金分割"，我国也有记载

虽然没有古希腊的早，但它是我国古代数学家独立创造的，后来传入了印度

经考证

欧洲的比例算法是源于我国而经过印度由阿拉伯传入欧洲的，而不是直接从古希腊传入的

因为它在造型艺术中具有美学价值，在工艺美术和日用品的长宽设计中，采用这一比值能够引起人们的美感，在实际生活中的应用也非常广泛，建筑物中某些线段的比就科学采用了黄金分割，舞台上的报幕员并不是站在舞台的正中央，而是偏在台上一侧，以站在舞台长度的黄金分割点的位置最美观，声音传播的最好

就连植物界也有采用黄金分割的地方，如果从一棵嫩枝的顶端向下看，就会看到叶子是按照黄金分割的规律排列着的

在很多科学实验中，选取方案常用一种优选法，它可以使我们合理地安排较少的试验次数找到合理的想法和合适的工艺条件

正因为它在建筑、文艺、工农业生产和科学实验中有着广泛而重要的应用，所以人们才珍贵地称它为"黄金分割"

黄金分割〔Golden Section〕是一种数学上的比例关系

黄金分割具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值

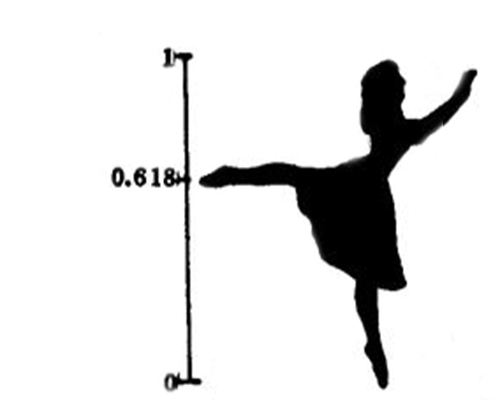
应用时一般取0.618 ，就像圆周率在应用时取3.14一样

发现历史由于公元前6世纪古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图，因此现代数学家们推断当时毕达哥拉斯学派已经触及甚至掌握了黄金分割

公元前4世纪，古希腊数学家欧多克索斯第一个系统研究了这一问题，并建立起比例理论

公元前300年前后欧几里得撰写《几何原本》时吸收了欧多克索斯的研究成果，进一步系统论述了黄金分割，成为最早的有关黄金分割的论著

中世纪后，黄金分割被披上神秘的外衣，意大利数家帕乔利称中末比为神圣比例，并专门为此著书立说

德国天文学家开普勒称黄金分割为神圣分割

到19世纪黄金分割这一名称才逐渐通行

黄金分割数有许多有趣的性质，人类对它的实际应用也很广泛

最著名的例子是优选学中的黄金分割法或0.618法，是由美国数学家基弗于1953年首先提出的，70年代在中国推广

教学中，取值为（√5－1）÷2，通常用希腊字母φ表示这个值

黄金分割奇妙之处，在于其比例与其倒数是一样的

例如：1.618的倒数是0.618，而1.618:1与1:0.618是一样的

确切值为(√5-1)/2 ，即黄金分割数

 黄金分割数是无理数，前面的1024位为:0.6180339887 4989484820 4586834365 6381177203 09179805762862135448 6227052604 6281890244 9707207204 18939113748475408807 5386891752 1266338622 2353693179 31800607667263544333 8908659593 9582905638 3226613199 28290267880675208766 8925017116 9620703222 1043216269 54862629631361443814 9758701220 3408058879 5445474924 61856953648644492410 4432077134 4947049565 8467885098 74339442212544877066 4780915884 6074998871 2400765217 05751797883416625624 9407589069 7040002812 1042762177 11177780531531714101 1704666599 1466979873 1761356006 70874807101317952368 9427521948 4353056783 0022878569 97829778347845878228 9110976250 0302696156 1700250464 33824377648610283831 2683303724 2926752631 1653392473 16711121158818638513 3162038400 5222165791 2866752946 54906811317159934323 5973494985 0904094762 1322298101 72610705961164562990 9816290555 2085247903 5240602017 27997471753427775927 7862561943 2082750513 1218156285 51222480939471234145 1702237358 0577278616 0086883829 52304592647878017889 9219902707 7690389532 1968198615 14378031499741106926 0886742962 2675756052 3172777520 35361393621076738937 6455606060 5922...下面的C++代码，可以计算任意精度的黄金分割数 （输出的数字都是准确值）：#include using namespace std;int main (void){    int d,e=2,i=0,j,k=10,N,m;    cout<<"请输入黄金分割数位数:\n",cin>>N,N++;    int *a=new int[2*N],*b=new int[N],*c=new int[2*N];    while(++i<2*N)a[i]=b[i/2]=c[i]=0;    for(cout<<"0.6",a[b=m=2]=4;--N>1;)    for(b[m]=e,d=0,j=k;--j+1&&!d;)    {        for(c[i=2*m]=j*j%k,e=j*j/k;--i>m-2;e=d/k)c[i]=(d=e+b[i-m+1]*j)%k;        for(i=d=m-1;i<2*m&&a[i]<=c[i];i++)(a[i]m-2;)if((a[i]-=c[i])<0)a[i]+=k,a[i-1]--;    }    delete a,delete b,delete c,cin.ignore(),cin.ignore();    return 0;}二、摄影·黄金分割法一幅优秀的摄影作品，不仅要有深刻的主题思想和内容，同时还应具备与内容相一致的优美形式和协调的构图

初学摄影，在取景时了解和掌握黄金分割法

对于提高作品美学价值很有帮助

黄金分割法，就是把一条直线段分成两部分，其中一部分对全部的比等于其余一部分对这一部分的比，常用2：3，3：5，5：8等近似值的比例关系迸引美术设计和摄影构图，这种比例也称黄金律

在摄影构图中，常使用的概略方法，就是在画面上横、竖各画两条与边平行、等分的直线，将画面分成9个相等的方块，称九宫图

直线和横线相交的4个点，称黄金分割点

根据经验，将主体景物安排在黄金分割点附近，能更好地发挥主体景物在图面上的组织作用，有利于周围景物的协调和联系，容易引起美感，产生较好的视觉效果，使主体景物更加鲜明、突出

另外，人们看图片和书刊有个习惯，就是由左向右移动，视线经过运动，往往视点落于右侧，所以在构图时把主要景物、醒目的形象安置在右边，更能收到良好的效果

初学摄影取景，可选选用“黄金分割法”的练习构图，经过多次实践，有了自己的经验和体会以后，就可根据实际情况自己进行创作了

如果都千篇一律，生搬硬套这一种形式，也不可取，时间久了反而会束缚自己的创作思想，使拍出的照片四平八稳，缺乏变化，贫乏无味，就谈不上有什么艺术性

用黄金分割法确定主体的位置，并没有完成构图的整个过程，还应注意安排必要的空间，考虑主体与陪体之间的呼应，充分表达主题的思想内容

同时，还要考虑影调，光线处理，色彩的表现等等

为了提高基本功，还有很重要的一点，就是要认真学习美学知识，加强美学修养，并通过拍摄实践，不断总结，积累经验，多拍出一些有较高艺术水平的照片来

图A如图A：“黄金分割”公式可以从一个正方形来推导，将正方形底边分成二等分，取中点X，以X为圆心，线段XY为半径作圆，其与底边直线的交点为Z点，这样将正方形延伸为一个比率为5︰8的矩形，（Y’点即为“黄金分割点”）， A︰C = B︰A = 5︰8

幸运的是，35MM胶片幅面的比率正好非常接近这种5︰8的比率（24︰36 = 5︰7.5）图B如图B：通过上述推导我们得到了一个被认为很完美的矩形，连接该矩形左上角和右下角作对角线，然后从右上角向Y’点（黄金分割点，见图A）作一线段交于对角线，这样就把矩形分成了三个不同的部分

现在，在理论上已经完成了黄金分割，下一步就可以将你所要拍摄的景物大致按照这三个区域去安排，也可以将示意图翻转180度或旋转90度来进行对照

三分法则“三分法则”实际上仅仅是“黄金分割”的简化版，其基本目的就是避免对称式构图，对称式构图通常把被摄物置于画面中央，这往往令人生厌

在图C1和C2中，可以看到与“黄金分割”相关的有四个点，用“十”字线标示

用“三分法则”来避免对称在使用中有两种基本方法，第一种：我们可以把画面划分成分别占1/3和2/3面积的两个区域

图C2第二种：直接参照图示的四个“黄金分割”点

例如，设想我们看到了非常引人入胜的风景，但缺少具有优美几何结构的被摄主体，这样拍出来的照片只会是一个空洞泛味的场景，那该如何处理呢？试着寻找一个与这种单调的环境形成鲜明对比的物体，并将这一被摄物置于如图C2中的其中一个“十”字点位置，这样照片就有了一个明显的锚点，并将观众的目光由此出发引导至整个风景

图D·树枝形成天然画框使山岩更为突出有时在我们看到的场景中有一个引人注目的被摄主体，但往往由于主体周围杂乱的环境分散了观众的注意力而削弱了主体的吸引力，使照片最终的效果令人很失望

试试寻找一个能够排除杂乱环境干扰的天然画框使观众注意力集中于被摄主体，如图D利用主体周围的树枝形成一个天然画框从而使中间的山岩更为突出

图F·小船和凉亭打破了原本泛味的对称交叉线/对角线实际上又是“黄金分割”的另一形式，其基本思想是提供了一条指引你视线的引导线，较为理想的是某两个边角之间的连线

传统的方法认为左上角是最好的起始点，因为大多数人习惯从这里开始浏览一幅图画（译者注：这一观点其实很多人看法不同）

但这种对角线如果是单一的直线往往会很平泛而令人厌烦，所以总要在图中有某种点缀（如图F）

以上内容由大学时代综合整理自互联网，实际情况请以官方资料为准。