中国数学史发展衰落这一时期指十四世纪中叶明王朝建立到明末的1582年
数学除珠算外出现全面衰弱的局面,当中涉及到中算的局限、十三世纪的考试制度中已删减数学内容、明代大兴八段考试制度等复杂的问题,不少中外数学史家仍探讨当中涉及的原因
明代最大的成就是珠算的普及,出现了许多珠算读本,及至程大位的《直指算法统宗》〔1592〕问世,珠算理论已成系统,标志着从筹算到珠算转变的完成

但由于珠算流行,筹算几乎绝迹,建立在筹算基础上的古代数学也逐渐失传,数学出现长期停滞
珠算珠算算法和口诀也逐渐趋于完善
例如王文素和程大位增加并改善撞归、起一口诀;徐心鲁和程大位增添加、减口诀并在除法中广泛应用归除,从而实现了珠算四则运算的全部口诀化;朱载墒和程大位把筹算开平方和开立方的方法应用到珠算,程大位用珠算解数字二次、三次方程等等
程大位的著作在国内外流传很广,影响很大
1582年,意大利传教士利玛窦到中国,1607年以后,他先后与徐光启翻译了《几何原本》前六卷、《测量法义》一卷,与李之藻编译《圜容较义》和《同文算指》
1629年,徐光启被礼部任命督修历法,在他主持下,编译《崇祯历书》137卷
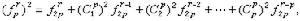
《崇祯历书》主要是介绍欧洲天文学家第谷的地心学说
作为这一学说的数学基础,希腊的几何学,欧洲玉山若干的三角学,以及纳皮尔算筹、伽利略比例规等计算工具也同时介绍进来
在传入的数学中,影响最大的是《几何原本》
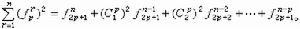
《几何原本》是中国第一部数学翻译著作,绝大部分数学名词都是首创,其中许多至今仍在沿用
徐光启认为对它“不必疑”、“不必改”,“举世无一人不当学”
满清侵入中原之后,科学再度被打入了“冷宫”
不但书的后半部分迟迟不能翻译,就连徐光启已经译出的上半部分也不再发行
西方传教士带来的科技著作,成为康熙、雍正或乾隆皇帝独享的业余爱好
其次应用最广的是三角学,介绍西方三角学的著作有《大测》《割圆八线表》和《测量全义》
《大测》主要说明三角八线(正弦、余弦、正切、余切、正割、余割、正矢、余矢)的性质,造表方法和用表方法
《测量全义》除增加一些《大测》所缺的平面三角外,比较重要的是积化和差公式和球面三角
所有这些,在当时历法工作中都是随译随用的
1646年,波兰传教士穆尼阁来华,跟随他学习西方科学的有薛凤柞、方中通等
穆尼阁去世后,薛凤柞据其所学,编成《历学会通》,想把中法西法融会贯通起来
《历学会通》中的数学内容主要有比例对数表》《比例四线新表》和《三角算法》
前两书是介绍英国数学家纳皮尔和布里格斯发明增修的对数
后一书除《崇祯历书》介绍的球面三角外,尚有半角公式、半弧公式、德氏比例式、纳氏比例式等
方中通所著《数度衍》对对数理论进行解释
对数的传入是十分重要,它在历法计算中立即就得到应用
清初学者研究中西数学有心得而著书传世的很多,影响较大的有王锡阐《图解》、梅文鼎《梅氏丛书辑要》(其中数学著作13种共40卷)、年希尧《视学》等
梅文鼎是集中西数学之大成者
他对传统数学中的线性方程组解法、勾股形解法和高次幂求正根方法等方面进行整理和研究,年希尧的《视学》是中国第一部介绍西方透视学的著作
清康熙重视西方科学,但只是作为自己的爱好
1712年康熙命梅彀成任蒙养斋汇编官,会同陈厚耀、何国宗、明安图、杨道声等编纂天文算法书
1721年完成《律历渊源》100卷,以康熙“御定”的名义于1723年出版
其中《数理精蕴》主要由梅彀成负责,分上下两编,上编包括《几何原本》《算法原本》,均译自法文著作;下编包括算术、代数、平面几何平面三角、立体几何等初等数学,附有素数表、对数表和三角函数表
由于它是一部比较全面的初等数学百科全书,并有康熙“御定”的名义,因此对当时数学研究有一定影响
清代数学家对西方数学做了大量的会通工作,并取得许多独创性的成果
这些成果,如和传统数学比较,是有进步的,但和同时代的西方比较则明显落后了
雍正即位以后,对外闭关自守,导致西方科学停止输入中国,对内实行高压政策,致使一般学者既不能接触西方数学,又不敢过问经世致用之学,因而埋头于究治古籍
乾嘉年间逐渐形成一个以考据学为主的乾嘉学派
随着《算经十书》与宋元数学著作的收集与注释,出现了一个研究传统数学的高潮
其中能突破旧有框框并有发明创造的有焦循、汪莱、李锐、李善兰等
他们的工作,和宋元时代的代数学比较是有进步的;和西方代数学比较,在时间上晚了一些,但这些成果是在没有受到西方近代数学的影响下独立得到的
与传统数学研究出现高潮的同时,阮元与李锐等编写了一部天文数学家传记—《畴人传》,收集了从黄帝时期到嘉庆四年已故的天文学家和数学家270余人(其中有数学著作传世的不足50人),和明末以来介绍西方天文数学的传教士41人
1840年鸦片战争以后,西方近代数学开始传入中国
首先是英人在上海设立墨海书馆,介绍西方数学
第二次鸦片战争后,曾国藩、李鸿章等官僚集团开展“洋务运动”,也主张介绍和学习西方数学,组织翻译了一批近代数学著作
其中较重要的有李善兰与伟烈亚力翻译的《代数学》《代微积拾级》;华蘅芳与英人傅兰雅合译的《代数术》《微积溯源》《决疑数学》;邹立文与狄考文编译的《形学备旨》《代数备旨》《笔算数学》;谢洪赉与潘慎文合译的《代形合参》《八线备旨》等等
《代微积拾级》是中国第一部微积分学译本;《代数学》是英国数学家德·摩根所著的符号代数学译本;《决疑数学》是第一部概率论译本
在这些译著中,创造了许多数学名词和术语,至今还在应用,但所用数学符号一般已被淘汰了
戊戌变法以后,各地兴办新法学校,上述一些著作便成为主要教科书
在翻译西方数学著作的同时,中国学者也进行一些研究,写出一些著作,较重要的有李善兰的《尖锥变法解》《考数根法》;夏弯翔的《洞方术图解》《致曲术》《致曲图解》等等,都是会通中西学术思想的研究成果
由于输入的近代数学需要一个消化吸收的过程,加上清末统治者十分腐败,在太平天国运动的冲击下,在列强的掠夺下,焦头烂额,无暇顾及数学研究
直到1919年五四运动以后,中国近代数学的研究才真正开始
整理研究雍正即位(1723)以后,对外闭关自守,导致西方科学停止输入中国,对内对汉族士大夫实行高压政策
1773年开设四库全书馆,辑录《永乐大典》保存佚书和征集私家藏书,于1781年编成《四库全书》,先后收集到《算经十书》和宋元时期的数学著作
纂修兼分校官戴震(1724~1777)对《周髀算经》《九章算术》《孙子算经》《五经算术》 4部著作详加校勘,改正许多误文夺字,对学者是有帮助的
随后,李潢(?~1811)著的《九章算术细草图说》9卷,《海岛算经细草图说》1卷和《辑古算经考注》2卷,李锐注的《数书九章》、《测圆海镜》和《益古演段》,沈钦裴著的《四元玉鉴细草》2 卷(1829)和罗士琳撰的《四元玉鉴细草》24卷(1834)都很有参考价值
焦循在《加减乘除释》(1798)中,用甲、乙、丙、丁……等天干字表示具体的数,列出加、减、乘、除的几个基本定律,用这些符号和定律来说明古代算法原理,这在中国数学史上是一个创造
汪莱著有《衡斋算学》 7册(1796~1805)
在第五册(1801)中,他讨论了二次、三次方程有多少正根以及正根和系数的关系问题,得到与韦达定理相当的结果
在第七册(1805)中专门讨论三项方程xn-pxm+q=0(n>m 都是正整数,p、q都是正数),他用归纳法得到上述方程有正根的条件相当于1802年李锐见到汪莱的《衡斋算学》第五册算书后,写了“第五册算书跋”,提出n次高次方程只有一个正根与多于一个正根和方程系数的符号有关,和得到一个正根后的(n-1)次方程的系数符号有关,他的结论基本上是正确的
在《开方说》(1817)中李锐进一步指出:高次方程系数符号变化一次的有1正根,变化二次的有2正根,变化三次的有3正根或1正根,变化四次的有4正根或2正根,所缺正根称为“无数”,“凡无数必两,无一无数者”
这些与笛卡儿的符号规则基本相同
他还指出:二次方程有2根,三次方程有3根或1根,四次方程有4根或2根(以上均包括负根);若方程有正、负根,将方程系数的正负号隔位易之,则正负根互换符号;方程的重根与“无数”不同等等
汪莱、李锐的工作,和宋元时代的代数学比较是青出于蓝而胜于蓝的;和西方代数学比较,在时间上晚了一些,但他们的成果是在没有受到西方近代数学的影响下独立得到的
对朱世杰的垛积术进行研究并有重大成果的是李善兰,在《垛积比类》(约1859)中,李善兰创造了一个著名的恒等式:利用三角垛求和公式就得出一个中外驰名的三角自乘垛求和公式:与传统数学研究出现高潮的同时,阮元与李锐等编写了一部天文数学家传记──《畴人传》(1795~1810)
《畴人传》收集从黄帝时期到嘉庆四年(1799)已故的天文学家和数学家270余人(其中有数学著作传世的不足50人)和明末以来介绍西方天文数学的传教士 41人
这部著作全由“掇拾史书,荃萃群籍,甄而录之”而成,收集的完全是第一手的原始资料,在学术界颇有影响
传统数学乾嘉年间形成一个以考据学为主的乾嘉学派,编成《四库全书》,其中数学著作有《算经十书》和宋元时期的著作,为保存濒于湮没的数学典籍做出重要贡献
在研究传统数学时,许多数学家还有发明创造,例如有“谈天三友”之称的焦循、汪莱及李锐作出不少重要的工作
李善兰在《垛积比类》〔约1859〕中得到三角自乘垛求和公式,称之为“李善兰恒等式”
这些工作较宋元时期的数学进了一步
阮元、李锐等人编写了一部天文学家和数学家传记《畴人传》46卷〔1795-1810〕,开数学史研究之先河
以上内容由大学时代综合整理自互联网,实际情况请以官方资料为准。